조선시대의 수학문제와 풀이법

2016년 7월 25일 (월) 사백서른일곱 번째 이야기 조선시대의 수학 문제와 풀이법(5) 번역문 문: 지금 갑・을・병・정・무 다섯 곳에서 곡식 2,000섬을 함께 부담하여 납부지까지 운송하되, 농지 면적, 납부지까지 운송거리, 곡식값을 고려하여 균등하게 부담하여 운송하려고 한다. 다섯 곳의 조건은 다음과 같다. 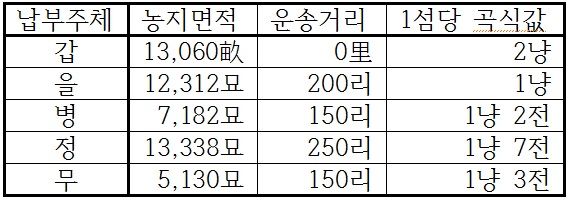      곡식 1섬을 1리 운송할 때 드는 수레 비용은 4리(釐)이다. 각 고을에서 운송해야 할 곡식은 얼마씩인가?   답: 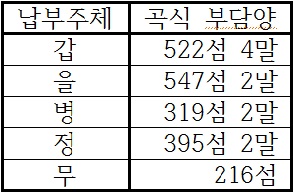    원문 今有甲·乙·丙·丁·戊五處, 共輸粟二千石, 以田地多寡·道里遠近·粟價貴賤, 均輸之. 甲田一萬三千零六十畝, 粟每石價二兩, 自輸本處; 乙田一萬二千三百十二畝, 粟每石價一兩, 至輸所二百里; 丙田七千一百八十二畝, 粟每石價一兩二錢, 至輸所一百五十里; 丁田一萬三千三百三十八畝, 粟每石價一兩七錢, 至輸所二百五十里; 戊田五千一百三十畝, 粟每石價一兩三錢, 至輸所一百五十里. 每石每里車價四釐. 問: 各處所輸若干? 答曰: 甲五百二十二石四斗, 乙五百四十七石二斗, 丙三百十九石二斗 丁三百九十五石二斗 戊二百十六石 - 19세기 조선의 대표적 천문ㆍ산학가 중 한 사람인 남병길(南秉吉, 1820~1869)의 수학서 『산학정의(算學正義)』 ‘화수차분(和數差分)’의 넷째 예제 해설      위 예제는 『구장산술(九章算術)』의 전형적인 균수술(均輸術) 문제를 바탕으로 조건을 다소 변경한 것이다.      균수술은 운송(또는 이동) 비용을 포함한 조세(또는 군역) 부담 전체를 고르게 배정하는 계산법으로, 『구장산술』에서는 난이도 상급의 비례산법이다. 균수술 문제는 각 고을의 운송거리가 문제의 조건으로 주어지는데, 이를 제거하면 최분술(衰分術 비례배분 산법)과 차이가 없게 된다. 이 때문에 남병길의 『산학정의』에서는 이를 ‘화수차분(和數差分)’조에 포함함으로써, 균수술을 최분술의 특수 형태로 취급하였다.      ‘화수(和數)’는 ‘수량의 합[和]’이고, 차분(差分)은 최분(衰分)을 달리 일컫는 말이다. 청나라 강희제(康熙帝) 때 전통수학과 서구수학의 우수한 점을 모아 집대성한 『수리정온(數理精蘊)』에서는 『구장산술』의 최분술을 여러 가지 비례(比例) 산법 중 하나로 위치지어 ‘화수비례(和數比例 수의 총합[和]을 이용한 비례 산법)’라고 하였다. 당시는 서구 수학의 내용 중 적용 범위가 가장 넓고 우수한 것 중 하나로 비례식을 꼽고 전통 수학의 여러 산법을 비례식으로 설명하였는데, 이것도 그 일례이다.      『산학정의』는 『수리정온』이 조선에서 정규 산학 과목으로 채택된(1791) 지 2세대 이상이 흐른 시점(1867)에 송·원대의 산학을 정점으로 하는 전통 산학을 『수리정온』의 체계에 따라 종합 정리한 책이다. 남병길은 옛 수학서들에 담긴 내용은 완전한데 산법이 확연히 드러나지 않고 표현이 어려워 후학들이 배우기 어렵다는 점을 이 책의 저술 동기로 언급하였다.      『산학정의』의 ‘화수차분’은 『수리정온』의 ‘화수비례’와 『구장산술』의 ‘최분’을 절충한 용어인데, 여기에도 서구 수학의 방법을 대폭 수용하여 전통 산법을 확연히 드러내려 한 남병길의 의도가 드러나 있다. ‘화수차분’은 곧 ‘화수비례’로 설명되는 전통 산법의 ‘차분술’이라는 말이다. 다시 말해 최분술(차분술), 화수비례, 화수차분는 모두 다음과 같은 비례 관계를 이용한다는 점에서 근본적으로 같다.         각항 배분율의 총합[和] : 배분할 사물의 총량=각항의 배분율 : 각항의 배분량      균수술은 각항의 배분율을 산출할 때 거리의 조건이 필수적으로 반영된다는 점이 일반적인 최분술 문제와 다른 점이다. 고대 국가에서 조세와 요역 및 군역의 배정과 수취는 국가 경영에 중요하고도 매우 비중이 큰 영역이었기 때문에 『구장산술』에서는 독립적인 산법으로 자리 잡았다.      위 예제에 대한 『산학정의』의 풀잇법을 현대 수식과 보충 설명을 가미하여 옮기면 다음과 같다. 계산의 큰 얼개는, 먼저 각 고을의 조건이 반영된 고을별 부담률을 산출하고 나서, 총 부담량 2,000섬을 이 비율에 따라 배분함으로써 고을별 부담량을 산출하는 것이다.      각 고을이 조세를 공평하게 분담하려면 농지면적이 클수록 많이 부담해야 하고, 운반하는 데 비용이 많이 들수록 부담을 경감시켜 줘야 하며, 곡식값이 비쌀수록 곡식을 마련하는 데 많은 비용이 들므로 부담을 경감시켜 줘야 한다. 따라서 농지면적은 부담률과 비례하고, 거리에 따른 운반비용과 곡식값은 부담률과 반비례한다.        이에 따르면 다섯 고을의 부담률은 다음과 같이 계산된다.(단, 1兩=10錢=100分=1000釐)          각 고을의 부담률을 총합하면(653+684+399+494+270=) 2,500이 되므로 다음의 비례를 이용하여,       부담률 총합 : 부담 총량=각 고을 부담률 : 각 고을 부담량  ……② 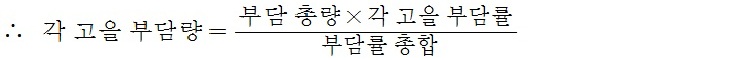    각 고을의 부담량이 구해지고,          이를 총합하면 2,000섬이 되어 문제의 조건에 합치한다.   『산학정의』의 위 풀이는 ②의 비례식을 금유술(今有術)로 대체하기만 하면 『구장산술』 균수술의 전형적인 계산 과정과 일치하는데, ①식 이상에 거리를 고려하는 균수술의 특징이 드러나 있고, ②식 이하는 전형적인 최분술의 산법과 동일하다. 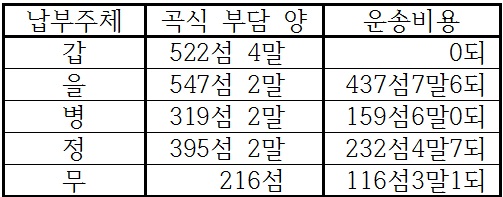       한편, 을 ·병·정·무 네 고을은 별도로 운송비용을 부담해야 하는데, 이를 곡식 수량으로 환산하여 각 고을의 부담량과 비교하면 오른쪽 표와 같이 그 비중이 상당함을 알 수 있다.       고대의 전통 수학서는 문제에 제시된 조건들이 당대의 사회경제적 현실을 상당정도 반영한다고 알려져 있다. 그런데 위 예제는 ㉠『구장산술』 균수장 셋째 예제에서 본디 호수(戶數)이던 것이 농지면적의 묘수(畝數)로, ㉡본디 갑의 호수가 20,520호이던 것이 묘수 13,060묘로, ㉢본디 다섯 고을의 총부담량이 10,000섬이던 것이 2,000섬으로 바뀌어 제시된 것을 제외하면 모든 수치 조건이 『구장산술』의 예제와 동일하다.      이로 볼 때 위 예제는 남병길이 『구장산술』 균수술 셋째 예제를 활용하되 課稅 대상을 당시 실정에 맞게 바꾸고(㉠) 계산이 깔끔하게 떨어지도록(『구장산술』의 답은 모두 복잡한 분수로 나왔다.) 수치를 조정한(㉡·㉢) 것임이 분명하다. 그렇다면 위 예제에는 남병길 당시의 사회경제적 상황뿐만 아니라 진(秦)·한(漢) 시대의 상황 및 현실과 무관하게 인위적으로 조정된 수치도 복합적으로 포함되어 있다. 예제의 내력을 잘 살펴야 하는 까닭이다. 글쓴이강민정 성균관대학교 대동문화연구원 수석연구원   주요 번역서 및 논문 『승정원일기』(인조/고종대) 번역에 참여 『무명자집』,『명고전집』,『농암집』,『북학 또 하나의 보고서, 설수외사』,『주석학개론』,『교감학개론』등 번역에 참여 『구장술해(九章術解)』의 연구와 역주, 성균관대학교 박사학위논문, 2015 외 다수